By Ellie Brown, Subeditor
A 65-year-old maths puzzle has been solved thanks to a team co-led by a University of Bristol Pure Mathematics professor.
Devised in Cambridge in 1954, the problem – an example of a Diophantine equation – proposed that every number from one to 100 can be expressed as the sum of three cubes.
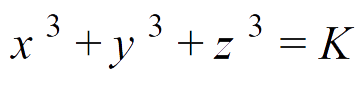
By March 2019, solutions had been found for almost all the numbers, with only 33 and 42 left. Professor Andrew Booker, inspired by a YouTube video on the problem, then devised a plan to finally solve it, using supercomputers at the University of Bristol.

Within three weeks, Booker’s algorithms and computer calculations resulted in success, as the answers for 33 were discovered. The number 42 was more challenging, so he enlisted the help of the record-breaking computers at MIT, along with Professor Andrew Sutherland of that institution. Together, with the help of Charity Drive they created a worldwide supercomputer, the solutions to 42 – ‘the meaning of life, the university, and everything’ for Douglas Adams fans – were found.
Speaking to Epigram, Professor Booker said: ‘The three cubes problem is interesting because it seems to be right at this boundary. It’s close to things that we understand very well, but the question of whether every eligible number has solutions to the three cubes problem could have been undecidable. For instance, if we had two variables instead of three, or if we had squares instead of cubes, it is easy to understand [and solve].
‘It has long been known that there are maths problems that are easy to state but wickedly hard to solve. Finding solutions for 33 or 42 does not answer these fundamental questions, but it gives another data point that we can use to make an educated guess.
‘It's only by going to these extremes that the true nature of the problem reveals itself.’
Despite the problem’s importance in number theory and the philosophy of maths, Professor Booker’s motivation to solve it was just as much ‘a case of serendipity’.
‘I ran a maths club at my kids' primary school, and I was looking for topics to present in that when I came across the second video [on YouTube], about [solving the three cubes equation for] number 74, and that got me hooked on the problem.’
He praised YouTuber Brady Haran, whose channel is called Numberphile, for his videos on the puzzle, saying he ‘played a part in the solutions to 74, 33 and 42 that was as important as anyone’s.’
‘Each video gave just the boost that was needed to solve the next problem. It’s likely that [the problem] would have been solved eventually anyway, but possibly not for decades.’
For more on the history of Diophantine equations, Booker recommends this page. You can also watch his videos explaining the problem in more depth here.
Feature image: Unsplash / Jan Laugesen
What are your favourite supposedly unsolvable maths problems? Let us know!







